4E電子通信実験(2001年度)
TTLゲートを用いた無安定マルチバイブレータ
最終更新日:2001.11.21
by M.Yanaka
1.目的
TTLゲートとCRとを用いて構成した無安定マルチバイブレータについて,特性を測定し,動作を理解する.
2.原理
TTLは,本来は論理回路を作るのに使われるものではあるが,その内部を見れば,トランジスタ,ダイオード,抵抗などから構成されていて,通常の電子回路と何ら異なるものではない.すなわち,本来の機能とは異なった使い方をして,信号発生器,波形整形回路等を作ることができる.本実験では,NANDゲート(7400)を用いた無安定マルチバイブレータについて調べてみる.
7400を用いた無安定マルチバイブレータの回路構成には種々のものがある[1]が,これらの回路のほとんどは経験的に得られたものであり,その動作機構は非常に複雑で,完全に解析されているわけではない.しかし,これらはいずれも良く知られた回路であり広く実用されている.
代表的な回路とその動作波形を図1〜4に示す.囲中のcont入力は発振を制御する端子である.発振きせるときに"1"を与え,発振させないときに"0"を与える.
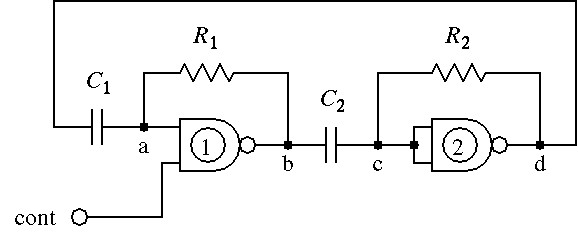
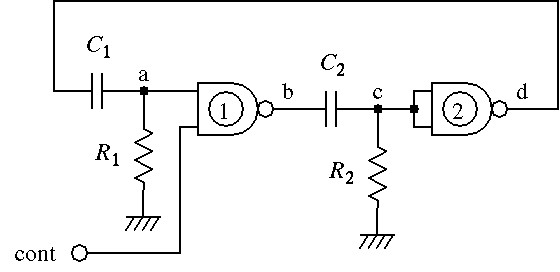
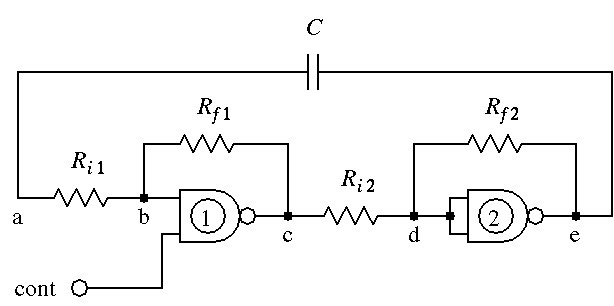
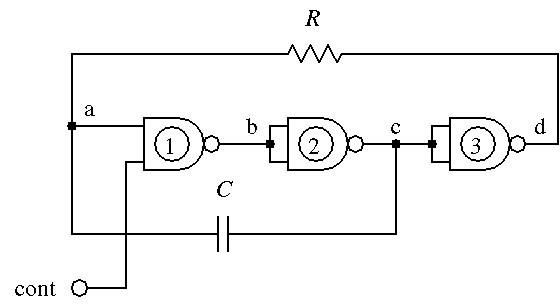
図1の回路は,モれぞれR1,R2でフィードバックをかけた2個のNANDゲートを,C1,C2で結合した構成になっている.図2は,2個のゲートを微分回路で結合した構成の回路である.図3は,Ri,Rfでフィードバックをかけてゲートの入出力特性を線形に近付けた回路を,2個つないで,更にCでフィードバックをかけたものである.図4の回路は,2個のゲートでつくった非反転バッファに1個の反転バッファをつなぎ,CRで作った積分回路でフィードバックをかけたものである.Cの一端を接地しないでc点に接続したのは,非反転バッファにヒステリシス特性を持たせるためである.
図 1
|

|
| (a) | (b) |
図1の回路について,動作の概略を説明する[2].
contが"0"(L電位)のときには,回路中のa,b,c,d点の電位は,それぞれH,H,H,Lとなり,回路は安定状態となろ.ただし,c点はスレショールド電位(1.4V)に近い値である.c点とd点の電位差はR2を流れる電流によって保たれている.
contが"1"(H電位)になると,その瞬間に,b点がL電位になり,C2で結合したc点もL電位となる.したがって,a,b,c,d点の電位は,それぞれH,L,L,Hとなる.しかし,c= L,d= Hという状態は不安定であり,2の入力抵抗とR2を通してC2が充電され,やがてc点はスレショ−ルド電位を越える.すると今度は,その瞬間に,d,a点がL電位に,b,c点がH電位になって状態が反転する.このa= L,b= Hという状態も不安定であり,やがてC1が充電されて,a点がスレショ−ルド電位を越えることによって,再び,状態が反転する.これらの状態の変化が繰り返されて,この回路は発振する.
以上に説明した回路の動作は,R1,R2,C1,C2がある値の範囲にあう場合にだけ起こることである.もし,これらの素子の値がこの範囲内でないときには,回路は別の機構によって発振したり,あるいは発振が不安定になったり,全く発振しなくなったりする.ちなみに,文献[3]によれば.図1の回路は7種類の発振モードを持つという.先に述べたのは,このうちの1つのモードだけである.
図 2
|

|
| (a) | (b) |
図2の回路について説明する[4].
contが"0"のときには,a,b,c,d点の電位はそれぞれL,H,L,Hで,回路は安定状態である.この状態からcont を"1"にしても回路は発振しない.発振させるには,何等かの雑音刺激が必要である.
例えば,C1の両端を瞬間的に短絡してやると回路は発振を始める.すなわち,短絡によって,a点をd点とを同電位(H)にし,H,L,L,Hという不安定な状態を作ってやるわけである.短絡を解除すると,a点はC1R1の時定数でL電位に向かい,やがて,スレショールド電位を越えて,b,c点がHに,d,a点がLになる.すると,今度はc点がC2R2の時定数でL電位に向かい,スレショールド電位を越えることによって,再び,状態が反転する.このようにして,回路は発振する.
図3,図4の回路については,動作の説明は省略するが,安定に発振する回路である[5].
図 3
|

|
| (a) | (b) |
図 4
|

|
| (a) | (b) |
回路の出力は,ゲートの出力端子から取り出せばよいのだが,波形が完全な矩形波になっていないので,実用的には,もう1段だけ,ゲートを通したものを利用するとよい.あるいは,ダイオードを用いて波形を改善することも可能である.
デューティ比50%のままで発振周波数を変えるには,回路中の抵抗やコンデンサの値を変えればよい.抵抗だけについていえば,図3のRf 2,図4のRの値を変えるだけでかなり広い範囲で発振周波数を変えることができる.それに対して,図1,図2の回路はR1,R2を同時に変えなければならないので多少は不便である.
これらの回路は,周囲温度,電源電圧の変動やlCのバラツキによって発振周波数が変動しやすく,設計通りの周波数が得られにくいという欠点がある.また,1MHz以上の発振も無理である.正確で安定な高周波発振を得るためには,水晶振動子を用いた水晶発振回路を使用するのが得策である.多くの実用回路では,水晶発振回路が使われている.
3.使用器具・部品
(1)ブレッドボード,
(2)直流安定化電源,
(3)シンクロスコープ,
(4)TTLIC(7400),
(5)抵抗,コンデンサ各種.
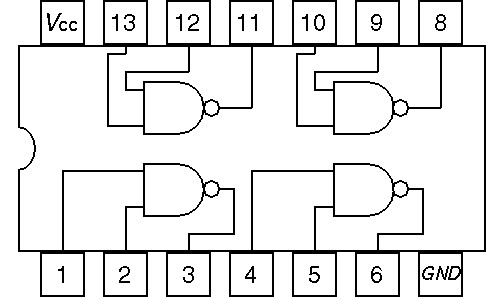
7400のピン配置を図5に示す.
図 5
|
4.実験方法
4.1 図1の回路について実験を行なう.
| (1) |
R1,R2 = 1kΩ;C1,C2 = 0.01μFにして回路を組み立て,cont = "0"のときの各部の電圧を測定する.つぎに,cont = "1"にして,各部の波形を観測し,記録する.
|
| (2) |
R1,R2を変えたときの発振周波数の変化を測定する.ただし,R1 = R2とする.
|
| (3) |
C1,C2を変えたときの発振周波数の変化を測定する.ただし,C1 = C2とする.
|
| (4) |
電源電圧VCCを変えたときの発振周波数の変化を測定する.ただし,VCCはICの定格の範囲内(4.5〜5.5V)で変化させること.
|
4.2 図2の回路について実験を行なう.
| (1) |
R1,R2 = 1kΩ;C1,C2 = 0.01μFにして回路を組み立て,cont = "0"のときの各部の電圧を測定する.つぎに,cont = "1"にして,各部の電圧を測定し,さらに,C1の両端を短絡して発振させ,各部の動作波形を観測し,記録する.
|
| (2) |
R1,R2を変えたときの発振周波数の変化を測定する.ただし,R1 = R2とする.
|
| (3) |
C1,C2を変えたときの発振周波数の変化を測定する.ただし,C1 = C2とする.
|
| (4) |
VCCを変えたときの発振周波数の変化を測定する.
|
4.3 図3の回路について実験を行なう.
| (1) |
Ri 1,Ri 2 = 220Ω;Rf 1,Rf 2 = 560Ω;C = 0.01μFにして回路を組み立て,cont = "0"のときの各部の電圧を測定する.つぎに,cont = "1"にして,各部の動作波形を観測し,記録する.
|
| (2) |
Rf 2を変えたときの発振周波数の変化を測定する.
|
| (3) |
Cを変えたときの発振周波数の変化を測定する.
|
| (4) |
VCCを変えたときの発振周波数の変化を測定する.
|
4.4 図4の回路について実験を行なう.
| (1) |
R = 1kΩ,C = 0.01μFにして回路を組み立て,cont = "0"のときの各部の電圧を測定する.つぎに,cont = "1"にして,各部の動作波形を観測し,記録する.
|
| (2) |
Rを変えたときの発振周波数の変化を測定する.
|
| (3) |
Cを変えたときの発振周波数の変化を測定する.
|
| (4) |
VCCを変えたときの発振周波数の変化を測定する.
|
5.質問事項
| (1) |
図3,図4の回路について,動作を説明せよ.
|
| (2) |
図1〜4以外の,IC(TTL,MOS)とCRを用いた無安定マルチバイブレータ回路について調べよ.
|
| (3) |
ICを用いた水晶発振回路や波形整形回路,単安定ルチバイブレータ,遅延回路等について調べよ.
|
6.文献
| [1] |
TTLアプリケーションマニュアル,テキサスインストルメントアジアリミテッド,pp.2-1〜2 (1972).
|
| [2] |
江村稔,高橋晴雄:パルス工学,pp.31〜34,コロナ社 (1983).
|
| [3] |
為貞建臣,山本博資:TTL-NANDゲートを用いた無安定マルチバイブレータの動作モード解析,信学論(D)J65-D-2,pp.218〜225 (1982).
|
| [4] |
佐藤清忠:実戦的ディジタル技術のすすめ—第13回 CR部品とTTL—,トランジスタ技術,1982-5.pp.356〜365 (1982).
|
| [5] |
荒牧成光,山路康貴:パルス・ディジタル回路,pp.215〜216,日本理工出版会 (1981).
|










